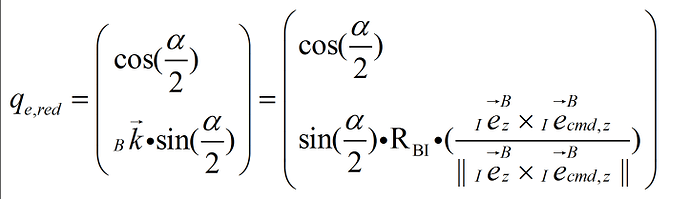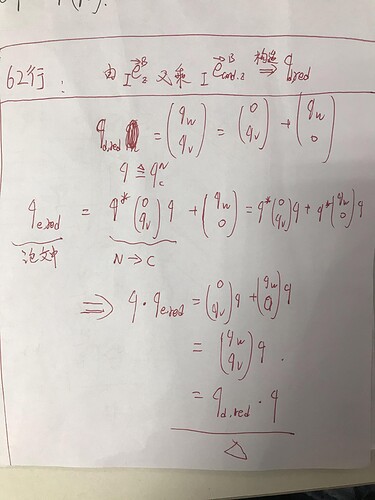I’m trying to understand the paper “Nonlinear Quadrocopter Attitude Control (2013)” referred by Pix4 in mc_att_control_main.cpp.I have a basic knowledge of quaterions and rotations,but i’m confused now.
1.in the paper Section 3.2.1 reduced attitude control , we can see formula (45) and (47):
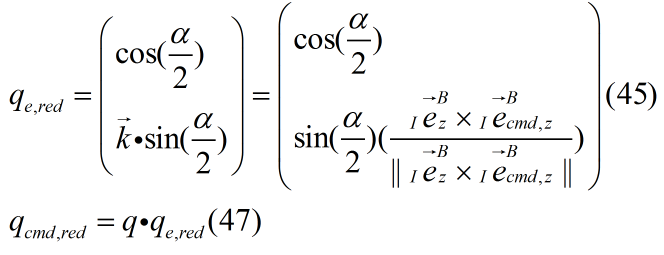
the qe,red refers to the rotation form current body attitude q to the reduced attitude qcmd,red , so ,why is vector k expressed in world frame I when world frame I isn’t the starting attitude? We don’t rotate the coordinate system by vector k using expressions based on world frame I,actually we rotate the coordinate system just based on the current attitude q.In my point of view, i think k should be rewritten in body frame.
2.in MulticopterAttitudeControl::control_attitude(float dt)
/* calculate reduced desired attitude neglecting vehicle’s yaw to prioritize roll and pitch */
Vector3f e_z = q.dcm_z();
Vector3f e_z_d = qd.dcm_z();
Quatf qd_red(e_z, e_z_d);
if (abs(qd_red(1)) > (1.f - 1e-5f) || abs(qd_red(2)) > (1.f - 1e-5f)) {
/* In the infinitesimal corner case where the vehicle and thrust have the completely opposite direction,
* full attitude control anyways generates no yaw input and directly takes the combination of
* roll and pitch leading to the correct desired yaw. Ignoring this case would still be totally safe and stable. */
qd_red = qd;
} else {
/* transform rotation from current to desired thrust vector into a world frame reduced desired attitude */
**qd_red *= q;**
}
In last line we can see qd_red=qd_redq , which can be seen as qd_red =qd_red * q,however in formula (47) the q is right-multiplied by qe,red . Maybe qd_red=qqd_red is right , for quaterions don’t satisfy commutative law.I hope the authors of the paper can see my questions.