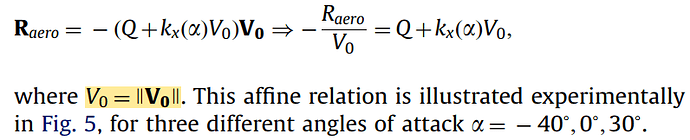Problem: The parasite drag formula used by this script (and the Firmware) seems incorrect because it violate the principle of force decomposition.
Maybe I’m missing some details, but the quadratic term 0.5 * rho * v_body[0] ** 2 * np.sign(v_body[0]) * x[1] in the aerodynamic coefficient estimation script:
seems inconsistent with the publication reference.
where V0 is the relative air velocity in the inertia frame. If my understanding is correct, the “v” in the drag equation should be the total relative airspeed (v = ||V0||, the length of V0, a scalar), NOT the velocity components at each axis.
Using the velocity component in this formula seems violate the principle of force decomposition.
Proof: If it is consistent with the principle, then both ways(see below) should get the same drag force/acceleration. Without loss of generality, we take X-axis drag acceleration for example:
- Calculate with Vx, the x-axis component of airspeed, just like the script and firmware does.
- Calculate the total drag acceleration with V0 first, then decompose it to get the reading at the X-axis.
The first way is straight forward because it already written in the script.
For the second way, since the body drag force (vector) has same direction with V0, the relative velocity to the air. Decomposing the drag acceleration along 3-axis (says the x axis) will get:
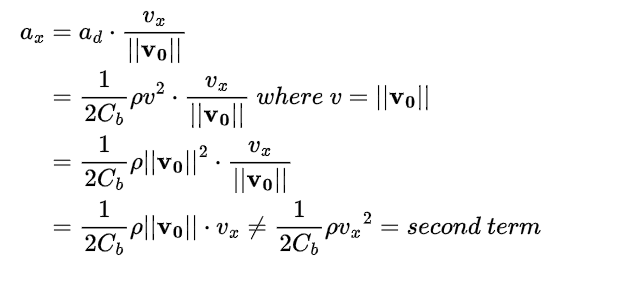
Because the norm (length) of a vector can greater than its component, the drag equation in the script may no longer hold if both axis has air flow simultaneously (wind from Northeast, for example).